误差函数、补误差函数、逆误差函数和累积分布函数

最近在写一个分布式的误差函数模块，所以进行了一些了解，整理在这里。误差函数是一种特殊函数，在概率、统计用到比较多。由于另外一个模块【累计分布函数】需要用到，所以在这里也一并介绍。

本文主要有三个内容：

什么是误差函数和逆误差函数
如何通过误差函数计算累积分布函数（CDF）
逆误差函数如何进行近似估计

误差函数：erf(error function)

是一种特殊函数，用于研究分布性质，定义如下：

$erf(x) = \frac{2}{\sqrt{\pi}} \int_0^{x}e^{-t^2}dt$

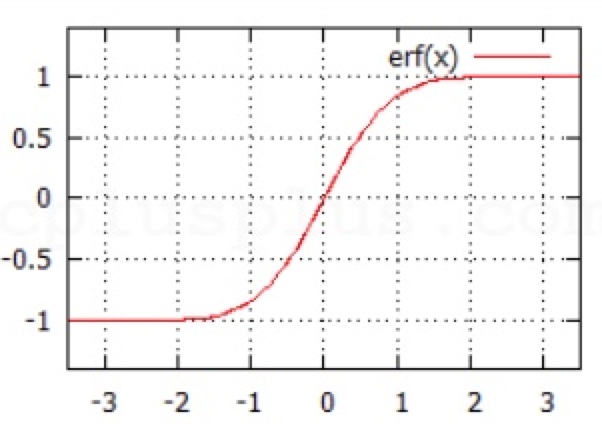
误差函数图像

C标准库中 math.h (C99) 和C++（Cmath，C++11）包含 erf 的实现。

C math.h

double erf  (double x);      
float erff (float x);
long double erfl (long double x);

C++ cmath

double erf (double x);      
float erf (float x);
long double erf (long double x);     
double erf (T x);           // additional overloads for integral types

使用误差函数

#include <stdio.h>  
#include <math.h>   
int main () {
    double x = 1.0;
    double result = erf(x);
    printf ("erf (%f) = %f\n", x, result );
    return 0;
}

性质：

奇函数：
$erf(-x) = -erf(x)$
复数
$erf(\overline{x}) = \overline{erf(x)}$

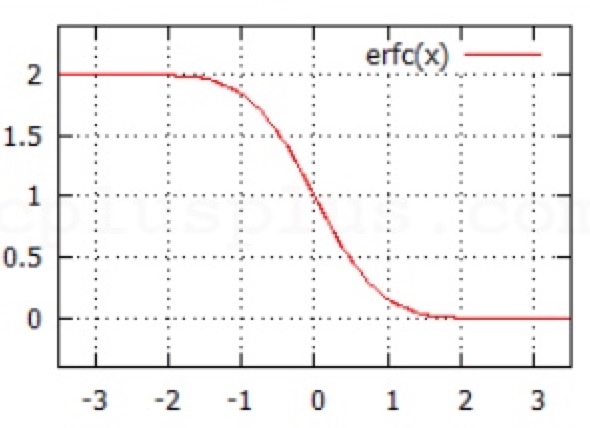
补误差函数：erfc(error function complementary)

取补，同样在math标准库中有实现（erfc等）

$erfc(x) = 1 - erf(x) = \frac{2}{\sqrt{\pi}} \int_{x}^{\infty}e^{-t^2}dt$

逆误差函数：erfinv(inverse error function)

$erf^{-1}(z)=erfc^{-1}(1-z)$

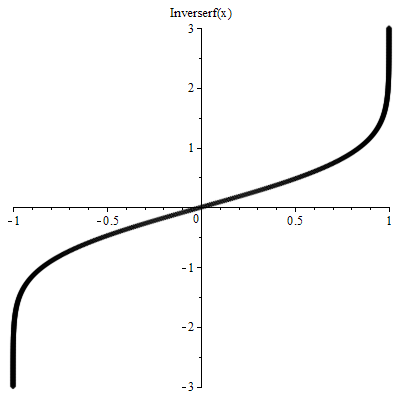
erf 的逆误差函数求解有很多种方法，通常使用近似估计。在
A handy approximation for the error function and its inverse这篇论文中，如下方法求解：

double erfinv(double x) {
    double sgn = (x < 0.0) ? -1.0 : 1.0;
    x = (1 - x) * (1 + x);
    double lnx = log(x);
    double tt1 = 2 / (M_PI * 0.147) + 0.5 * lnx;
    double tt2 = 1 / (0.147) * lnx;
    return(sgn * sqrt(-tt1 + sqrt(tt1 * tt1 - tt2)));
}

用误差函数计算正态分布的累积分布函数 CDF

正态分布的累积分布函数

$F(x) = \frac{1}{2}(1 + erf(\frac{x - \mu}{\sqrt{2}\sigma})) = \frac{1}{2} erfc(-\frac{x - \mu}{\sqrt{2}\sigma})$

标准正态分布的累积分布函数（可以直接把上面的公式 $\mu=0,\sigma=1$ ）

$\Phi(x) = \frac{1}{\sqrt{2\pi}} \int_{-\infty}^{x}e^{\frac{-t^2}{2}}dt= \frac{1}{2}[1+erf(\frac{x}{\sqrt{2}})] = \frac{1}{2}erfc(-\frac{x}{\sqrt{2}})$

// 正态分布
long double cumul_dist_func(double value, double mu, double sigma) {
    double param = 0.5;
    double t = (value - mu) / sigma * M_SQRT1_2;
    return param * erfc(-t);
}
// 标准正态分布
double standard_normal_CDF(double value) {
    return 0.5 * erfc(-value * M_SQRT1_2);
}

R 语言中的 erf 函数

install.packages("pracma")
library("pracma")
erf(x)