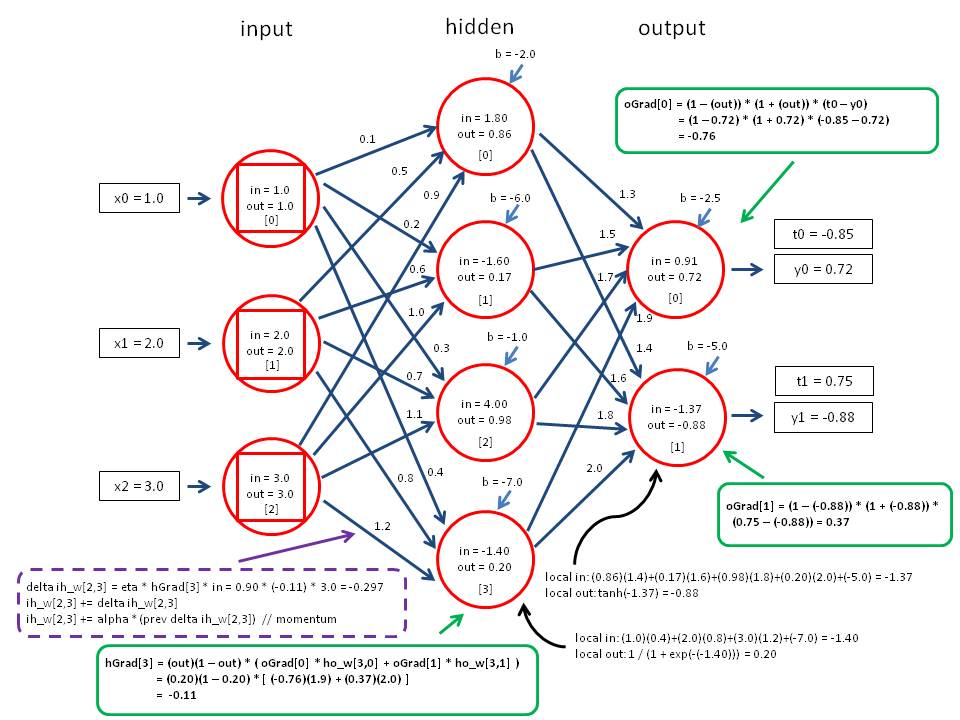
后向传播（back propagation）

这篇文章是复习《Data Mining: Concepts and Techniques》9.2节的内容。

后向传播算法是一种神经网络学习算法。

神经网络用一组连接的输入、输出单元，其中每个连接都与一个权重相关联。

神经网络可以用于分类（离散值），也可以用于预测（连续值）。

在学习阶段，调整权重，使其能够根据输入进行预测学习。因此神经网络的可解释性差，相当于一个黑盒。

神经网络和神经网络的算法有很多，这是其中一种。

9.2.1 按照多层前馈神经网络（后向传播算法在这种类型的网络上运行）
9.2.2 讨论定义网络拓扑
9.2.3 介绍后向传播
9.2.4 讨论训练后的神经网络提取规则

9.2.1 多层前馈神经网络（multilayer feed-forward）

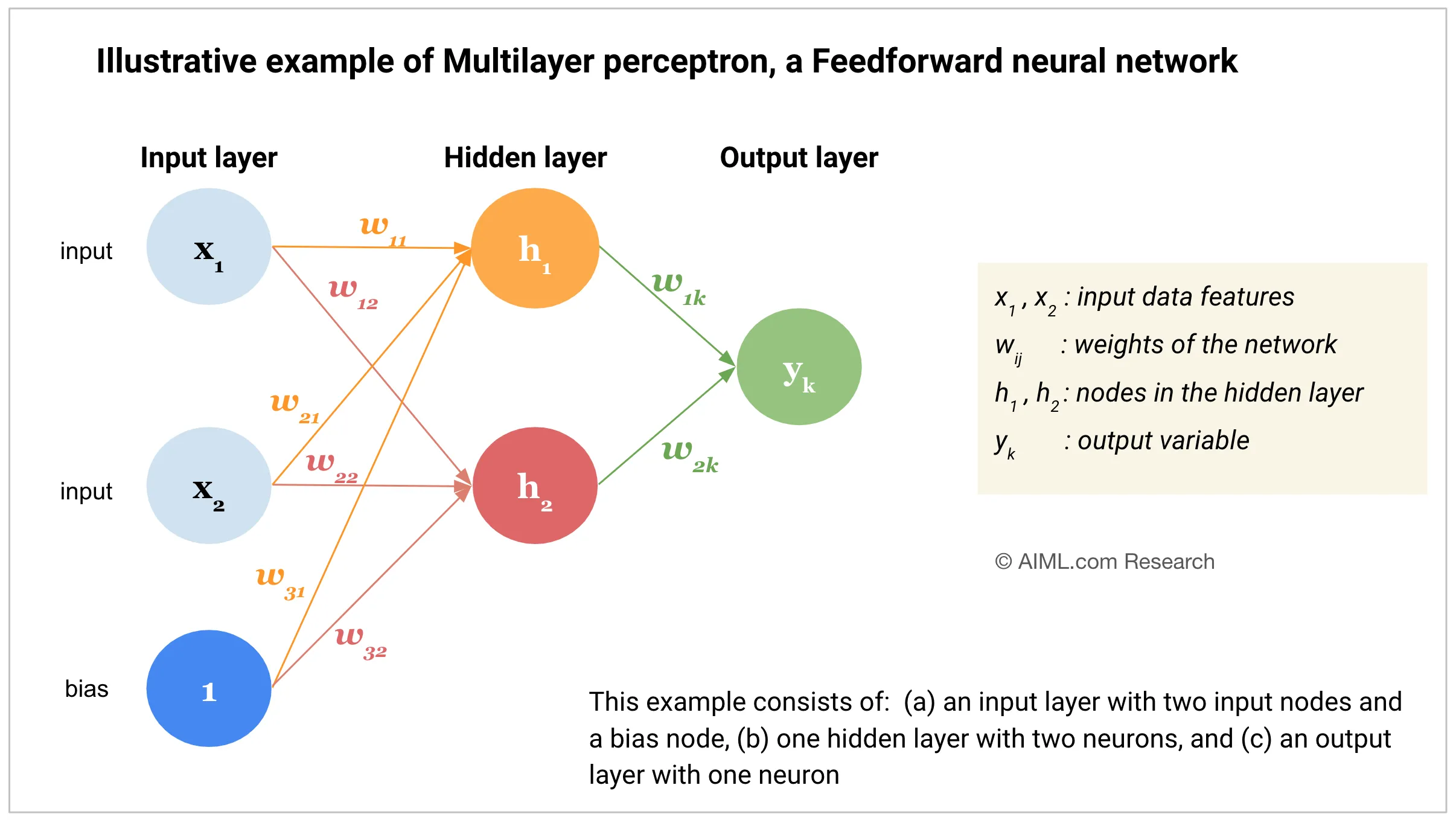
组成：一个输入层，N个隐藏层（上图例子中为1层），一个输出层。每层都由单元（神经节点、神经元）组成（图里的圈圈）。每个单元将输入值加权求和，将输出值提供给下一层。

每个单元取前一层单元输出的加权和作为输入。对这个加权和，再用一个非线性的激活函数（比如ReLU）计算，作为输入。非线性激活函数用于支持非线性的输入建模。（要不然全是线性关系）。

9.2.2 定义网络拓扑

9.2.3 后向传播

过程：

1. 初始化权重：网络的权重初始化为小随机数。每个单元还带一个bais（偏倚），这也是小随机数
2. 向前传播输入：
   1. 输入层：训练集通过输入层，不发生变化
   2. 隐藏层和输出层：
      1. 计算净输入：加权求和$I_j=\sum_{i}w_{ij}O_i+\theta_{j}$ 其中，$I_j$就是净输入，$w_{ij}$是上一层和单元i连接的权重值，$O_i$是上一层单元i的输出，$\theta_j$是单元j上的bias。
      2. 激活（activation）：其实就是把上一步具有线性关系的净输入变得非线性。这个也叫挤压函数，其实就是把输入值域范围变小到0到1之间。比如用logsitic函数。
         
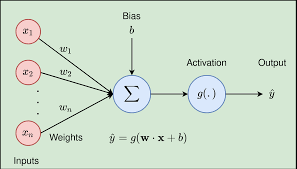
3. 向后传播误差：更新权重和bias。
   1. 输出层：对于输出层单元j，误差$Err_j=O_j(1-O_j)(T_j-O_j)$，其中$O_j$就是单元j实际的输出，$T_j$是之前训练集中的已知值（是一个目标值）。这里面$O_j(1-O_j)$是logistic函数的导数。
   2. 隐藏层：对于隐藏层单元j的误差，$Err_j=O_j(1-O_j)\sum_{k}Err_kw_{jk}$，其中，$w_{jk}$是单元j到之前一层（对于最后一个隐藏层，就是输出层，对于倒数第二个隐藏层，就是最后一个隐藏层）单元k的连接权重$Err_k$是k的误差。
   3. 更新权重和bias：
      1. $\triangle {w_{ij}} = (l)Err_jO_i, w_{ij} = w_{ij} + \triangle {w_{ij}}$其中，$\triangle {w_{ij}}$是权重的改变值。$l$是学习率，通常在0到1之间。
      2. $\triangle {\theta_j} = (l)Err_j, \theta_j=\theta_j+\triangle {\theta_j}$
4. 终止条件：
   1. $\triangle {w_{ij}}$小于阈值
   2. 如果用于分类，分类错误结果小于阈值
   3. 超过训练周期数

例子